 [Startseite] → [Projekte] → [Schwarmfische]
[Startseite] → [Projekte] → [Schwarmfische]
Bitte beziehen Sie sich auf den Artikel auf ResearchGate
Verringerung des Widerstands beim Schwimmen im Schwarm - ein CFD-Ansatz
Nils Owsianowski, Antonia B. Kesel
Bionik-Innovations-Centrum, Hochschule Bremen

Es gibt unterschiedliche Gründe, weshalb Fische Schwärme bilden. Neben den Aspekten des Schutzes, der Ernährung und der Fortpflanzung soll die Schwarmbildung außerdem die Effizienz bei der Fortbewegung verbessern. Diese Hypothese der Energieeinsparung durch die Schwarmbildung war bereits Gegenstand mehrerer Studien[1,2]. Schon 1973 beschrieb Weihs typische Muster für Fischschwärme, die große Entfernungen zurücklegen, insbesondere während der Wanderung. Nach seinem Modell entstehen zwischen einzelnen Fischen besonders vorteilhafte Konstellationen. Um der hohen Strömung im Kielwasser eines vorausschwimmenden Gruppenmitglieds auszuweichen, wird die eigene Position ungefähr um die Breite der entstehenden Wirbelstraße zur Seite verlagert. Auf diese Weise kann der Strömungswiderstand, je nach Position der Fische im Schwarm, um bis zu 30 % reduziert werden[3]. In dieser Studie wurden zweidimensionale numerische Simulationen mit bis zu neun Individuen durchgeführt, wobei der Schwerpunkt auf den Strömungsbedingungen und den Interaktionen zwischen einzelnen Individuen sowie der Widerstandsverteilung innerhalb des Schwarms lag. Zunächst wurde das Verhalten einzelner Fische und die Dynamik einer Gruppe experimentell erfasst. Mittel dieser Informationen konnte ein Optimierungsalgorithmus entwickelt werden, der zum Einen die Mechanismen und das Verhalten eines Schwarms nachbildet, und zum Anderen einen minimale Gesamtwiderstandzum Ziel hat. Des Weiteren zeigen dynamische Simulationen mit bewegtem Gittern die numerischen Ergebnisse der wellenförmigen Fortbewegung auf. Aufgrund der undulierenden Bewegung wird eine umgekehrte van-Kármán-Straße durch den Strömungskörper erzeugt. Durch die stark erhöhte Komplexität einer dynamischen Rechnung entsteht jedoch ein nahezu realistisches Modell eines schwimmenden Fischschwarms.
Video 1: Barschschwarm, aufgenommen im Strömungskanal.
Alle Iterationsschritte wurden mit CFD (Computational Fluid Dynamics) berechnet, wobei die Parametersteuerung und -bewertung durch einen evolutionären Algorithmus erfolgte. Es wurden unstrukturierte Netze mit bis zu 60.000 Elementen verwendet (berechnet im Jahr 2007). Zur Auflösung der Grenzschicht wurden mindestens zehn Prismenschichten um die Strömungskörper gelegt. Für die Optimierung wurde eine "Evolutionsstrategie"[4] gewählt. Sie folgte den Schritten Reproduktion (Kopie der vorherigen Generation), Mutation (zufällige Variation) und Selektion (Beibehaltung der besten Formation) gemäß Charles Darwins "survival of the fittest". Im vorliegenden Fall bedeutet dies, dass die Position jedes Individuums zufällig verändert wurde (normal verteilte Zufallszahlen), wobei der Algorithmus die resultierende Konstellation im Hinblick auf den Gesamtwiderstand der Gruppe bewertet. Verringert sich der Widerstand gegenüber der bisherigen Anordnung, bildet die neue Formation die Grundlage für weitere Evolutionsschritte.
Um das System zu testen und seine Funktionalität zu bewerten, wurden die passiven Strömungskörper mit den Ergebnissen von Experimenten im Strömungstank verglichen. Die Entwicklung von vier Körpern ergab eine gerade Ausrichtung (Video 2) als optimales Muster. Jeder Strömungskörper nahm einen Platz direkt hinter der Hinterkante eines anderen Strömungskörpers ein, mit Ausnahme des vorderen. Eine solche Anordnung wäre eigentlich zu erwarten, denn es gibt viele Bereiche, insbesondere im Rennsport, in denen die Nutzung des Windschattens besonders vorteilhaft ist.
Video 2: Das Ergebnis einer zweidimensionalen Entwicklung der Anordnung von vier passiven, stromlinienförmigen Körpern in Bezug auf den minimalen Gesamtwiderstand. Die Farbskala zeigt den Geschwindigkeitsverlauf von niedriger (blau) bis hoher Geschwindigkeit (rot).
Dies gilt jedoch nicht für Objekte, die sich aktiv durch ein Fluid bewegen. Aufgrund der Wechselwirkung zwischen dem schwimmenden Fisch und seiner Umgebung sieht die Kielwasserstruktur völlig anders aus. Um sich vorwärts bewegen zu können, muss der Fisch eine bestimmte Menge Wasser nach hinten beschleunigen. Als Folge dieser Schuberzeugung überschreiten Bereiche des Kielwassers sogar die Reisegeschwindigkeit. Unter der Annahme des Kontinuitätsgesetzes muss ein gleichmäßig schwimmender Fisch mit konstanter Geschwindigkeit seinen Strömungswiderstand kompensieren, indem er dabei einen exakt gleichgroßen Schub erzeugt. Ein vereinfachtes Modell eines aktiv schwimmenden Fisches ist ein Strömungskörper, der hinter sich einen Schubstrahl erzeugt. Daher wurde zunächst eine zusätzliche Geschwindigkeits-Randbedingung am Schwanz des Strömungskörpers implementiert. Der resultierende Schub wurde an den jeweiligen Strömungswiderstand des Körpers angepasst, sodass sich die Strömungskräfte bei konstanter Geschwindigkeit gegenseitig aufheben. Bei Simulationen mit vier bzw. sechs aktiven Strömungskörpern bilden sich deutliche Diamantanordnungen heraus, die einen leichten Versatz zu den jeweiligen Führungspositionen zeigt (Video 3 & 4).
Video 3: Entwicklung der Schwarmbildung von vier Individuen.
Video 4: Entwicklung der Schwarmbildung von six Individuen.
In einer zweidimensionalen Simulation hat jeder Strömungskörper zwei Freiheitsgrade (die x- und y-Koordinaten), sodass die Zahl der möglichen Konstellationen innerhalb eines Iterationsschritts mit der Zahl der Individuen steigt. Dies ist die Schwäche einer evolutionären Strategie, da die Anzahl der Generationen, die erforderlich sind, um ein Optimum zu erreichen, exponentiell ansteigt. Es besteht auch die Möglichkeit, dass der Algorithmus zu einem lokalen Optimum konvergiert. Normalerweise versucht man, solchen Sackgassen mit einer variablen Schrittweite zu entkommen, aber dieser zusätzliche Parameter erhöht wiederum die Mutationsmöglichkeiten. Während eine Evolution mit 4 Fischen noch etwa 100 Generationen braucht, um das Optimum zu erreichen, sind es bei 6 Fischen schon etwa 400 Generationen. Eine Evolution von 9 Fischen führte nicht direkt zu einer optimalen Konstellation, weshalb in diesem Fall ein zusätzlicher Ansatz des biologischen Verhaltens in den Algorithmus implementiert wurde. Dabei werden drei Mechanismen genutzt: Erstens: Nur etwa ein Viertel der gesamten Fischgruppe führt gleichzeitig einen relevanten Positionswechsel durch. Zweitens: Schwimmt ein Individuum in einer besonders günstigen Position, folgt es seinem führenden Artgenossen. Drittens: Interaktionen zwischen Individuen, wenn die Gefahr einer Kollision besteht. In diesem Fall weicht ein Individuum zur Seite, um einem herannahenden Artgenossen Platz zu machen. Selbst mit diesen drei zusätzlichen Einschränkungen dauerte es über 1500 Generationen, um ein Optimum von 9 Individuen zu erreichen. Auch hier zeigt sich eine klare Rautenstruktur mit leicht versetzten Positionen (Abbildung 1).
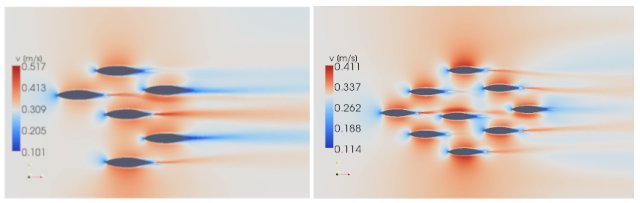
Abbildung 1: Die Ergebnisse der Optimierungen von sechs und neun Individuen. Die Farbskala zeigt des Geschwindigkeitsfeld in m/s an. Die Geschwindigkeit der Nachlaufströmung hängt von der erzeugten Schubkraft ab. Je höher die Geschwindigkeit ist, desto höher ist der erzeugte Schub und damit der Widerstand eines einzelnen Gruppenmitglieds.
Ein genauerer Blick auf die Widerstandsverteilung hilft, die Mechanismen besser zu verstehen, die die Struktur einer Schule bilden. Eine schematische Darstellung der Widerstandsverteilung ist in Abbildung 2 zu sehen. Es ist zu erkennen, dass der Widerstand eines Individuums stark von seiner Position innerhalb der Gruppe abhängt. Überraschenderweise ist der führende Fisch nicht zwangsläufig dem höchsten Widerstand ausgesetzt, und außerdem kann der Widerstand zwischen benachbarten Individuen stark variieren. Dies könnte ein Grund für die Dynamik und Instabilität der Schwarmbildung sein. Einzelne Individuen wechseln häufig ihre Position, entweder um unangenehmen Stellen zu entkommen oder um in einer günstigen Position zu bleiben.
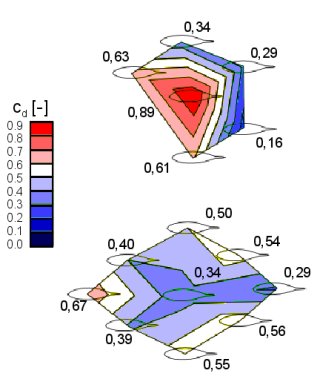
Abbildung 2: Schematische Darstellung der Widerstandsverteilung innerhalb der Schule. Der Widerstandsbeiwert ist neben der jeweiligen Position angegeben.
Das Strahlantriebsmodell scheint eine akzeptable Vereinfachung für die Simulation von Fischschwärmen zu sein. Das Strömungsfeld eines schwimmenden Fisches ist jedoch sehr viel komplexer. Das nächste Modell berücksichtigt die Kinematik und die wellenförmige Bewegung eines schwimmenden Fisches. Zu diesem Zweck wurde die Kinematik eines schwimmenden Fisches aus Videoaufnahmen abgeleitet und auf ein dynamisch bewegtes Gittermodell angewendet. Video 5 zeigt das Geschwindigkeitsfeld eines Schwarmes von vier Individuen, die in einer rautenförmigen Formation schwimmen. Es zeigt deutlich den Zickzackkurs des Nachstroms, der durch die umgekehrte van-Kármán-Straße erzeugt wird. Sie offenbart nicht nur die optimale Position, sondern auch neue Fragen zu Schwanzschlagfrequenzen, Amplituden und Wellenlängen. Um die zur Kompensation des Einzelwiderstands erforderliche Schuberzeugung anzupassen, wurde hier die Schlagfrequenz entsprechend angepasst.
Video 5: Dynamisches CFD-Modell eines aus vier Individuen bestehenden Schwarms. Die Farbskala zeigt das Geschwindigkeitsfeld.
Referenzen
[1] Belyayev, V. V. & Zuyev, G.V. (1969): Hydrodynamic hypothesis of school formation in fishes, Problems of Ichthyology: 9: 578-584.
[2] Partridge, B. L. (1983): The structure of schools of giant bluefin tuna in Cape Cod Bay, Exp. Biol. of Fishes: 9: 253-262.
[3] Weihs D. (1973): Hydrodynamics of Fish Schooling, Nature Vol. 241, 290-291.
[4] Rechenberg, I. (1994): Evolutionsstrategie ´94, Werkstatt Bionik und Evolutionstechnik, Band 1, Stuttgart: frommann-holzboog, ISBN: 3-7728-1641-X.
last update: 23 Nov 2023 19:00
