 [Startseite] → [Projekte] → [Schwimmende Schlangen]
[Startseite] → [Projekte] → [Schwimmende Schlangen]
Volltext der Arbeit ist verfügbar auf ResearchGate
Mathematische Modellierung und numerische Simulation der Fortbewegung von gliedmaßenlosen Organismen
Im Laufe der Evolution haben sich verschiedene Arten der Fortbewegung entwickelt, wobei jedes Lokomotionsprinzip perfekt an seine jeweiligen Anforderungen angepasst ist, Flügel zum Fliegen, Flossen zum Schwimmen und Beine bieten einen vernünftigen Kompromiss für die Fortbewegung an Land. Nur Schlangen und Würmer haben eine gliedmaßenlose Fortbewegung entwickelt, welche die Möglichkeit bietet, in unterschiedlichem Terrain mit ähnlicher Eleganz zurechtzukommen[1]. Sie sind nahezu unabhängig von den Umgebungsbedingungen, was das zugrundeliegende Prinzip der gliedmaßenlosen Fortbewegung für technische Anwendungen interessant macht. Bevor ein solches Prinzip auf technische Systeme übertragen werden kann, ist ein allgemeines Verständnis der zugrundeliegenden Biomechanik und der damit verbundenen mathematischen Beschreibung der Abläufe notwendig. Diese Arbeit verfolgt den Ansatz eines einfachen mathematischen Modells, das aus der Anatomie (Muskel-Skelett-Interaktion) und der neuronalen, kaskadischen Ansteuerung segmentierter Organismen abgeleitet ist. Es kombiniert die Vorteile der Schlängel- und Wellenbewegung von Schlangen und Fischen mit denen der peristaltischen Fortbewegung von Würmern. Dabei ist eine maßgebliche Anforderung, die einfache Beschreibung der Bewegung bzw. der Ansteuerung der Aktuatoren in linearen Gleichungen, damit kleine und kostengünstige Mikrocontroller diese schnell prozessieren können. Das Gleichungssystem beschreibt die jeweiligen Bewegungsmuster nur durch eine Reihe von Koeffizienten, die für die individuelle Bewegung bestimmt werden könne. Simulationen veranschaulichen das zugrundeliegende Modell und liefern die Basis für eine qualitative Bewertung.
Das Konzept basiert auf aneinandergereihten Dreieckprismen (Abb. 1), deren Längskanten drei Aktuatoren repräsentieren, die in zyklischen Dehnungen und Kontraktionen die Stirnflächen neigen. Um den Anforderungen gerecht zu werden, wird der Bewegungszyklus als vereinfachte lineare Stufenfunktion beschrieben (Abb. 2).
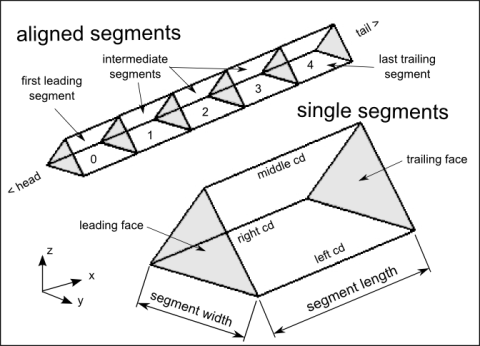
Abbildung 1: Illustration des allgemeinen Bauplans eines künstlichen Körpersegments. Ein Segment wird als dreieckiges Prisma mit zwei dreieckigen Stirnflächen abstrahiert, die durch drei Aktuatoren cd verbunden sind. Der Zusammenbau mehrerer ausgerichteter Segmente ergibt die Struktur eines langen und schmalen Modells.
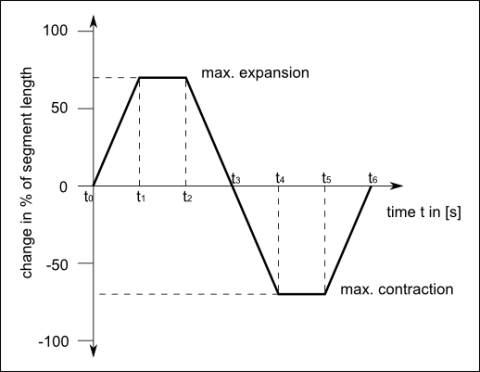
Abbildung 2: Prinzip eines Ausdehnungs-/Kontraktionszyklus’ der Aktuatoren. Das Ausmaß der Dehnung bzw. Die Längenänderung wird relative zur ursprünglichen Segmentlänge angegeben und über die Zeit ti in Sekunden aufgetragen. Der gesamte Zyklus wird über eine abschnittsweise definierte Funktion beschrieben. Jeder Abschnitt zwischen zwei Punkten ti und ti+1 ist durch eine lineare Funktion f(x)=mx+b beschrieben.
Diese stellen entweder Wirbeltiere mit einem starren Skelettelement und zwei antagonistischen Muskelsträngen oder drei Muskelstränge dar, die die Funktion der Ringmuskeln von wirbellosen Tieren übernehmen. So lassen sich sowohl seitliche Verschränkungen als auch Kontraktionen des Segments darstellen (Animation 1 & 2). Werden die Segmente in einer Reihe aneinandergehängt und ihre aufeinanderfolgenden, zyklischen Bewegungen zeitlich verzögert, kommt es zu Wellenbewegungen über den gesamten Strang. Für ein individuelles, zweidimensionales Bewegungsmuster sind nur zwei Komponenten relevant. Zum einen der Grad der Verformung, die Amplitude, also die Stärke der Dehnung oder Kontraktion der Aktuaoren. Zum anderen die zeitliche Verzögerung des Bewegungszyklus zwischen zwei aufeinanderfolgenden Segmenten. Beide Komponenten können sich entlang der Segmentreihe verändern.
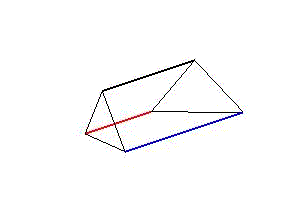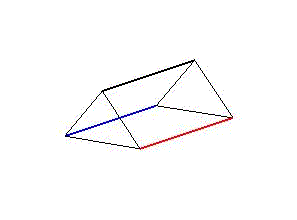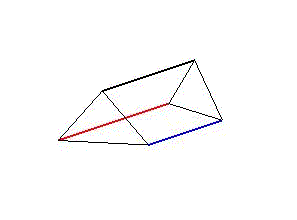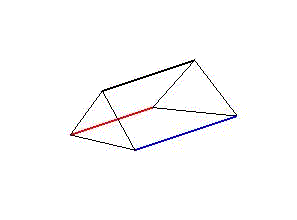
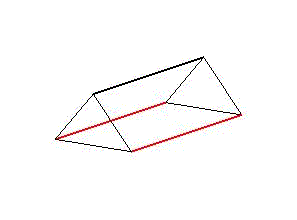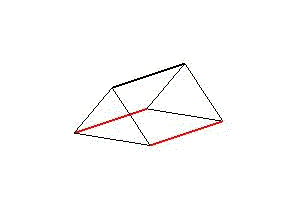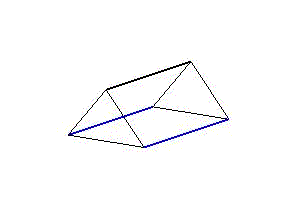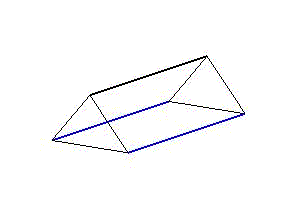
Animation 1: Schematische Darstellung der Segmentverformung während einer Wellenbewegung links und einer peristaltischen Bewegung rechts.
Diese Änderung wird als linear angenommen und jeweils durch zwei Koeffizienten m und b in der Gleichung f(x)=mx+b beschrieben. Während die Änderung der zeitlichen Verzögerung über die Segmentkette konstant ist und daher durch eine einzige Funktion beschrieben wird, wird die Längenänderung in drei Abschnitte unterteilt. Es gibt den Kopfabschnitt, den Mittelabschnitt und den Schwanzabschnitt. Letztlich können diese als die drei Abschnitte der Wirbelsäule betrachtet werden, die aus dem Hals-, Brust- und Lendenwirbelbereich besteht. Die Amplitude der Biegung wird also über drei Gleichungen mit sechs Koeffizienten bestimmt, die den jeweiligen Segmenten zugeordnet sind. Alle Koeffizienten lassen sich geometrisch aus Bildsequenzen von aufgenommenen Organismen ableiten. Dazu wird zunächst die Körperachse digitalisiert, spline-interpoliert und schließlich werden die Segmente trigonometrisch berechnet. Ihre Veränderung über die Zeit kann nun interpoliert werden (Abb. 3). Dabei ist zu beachten, dass die Länge und Breite der Segmente den Dimensionen der späteren Anwendung entsprechen.
![]()
Abbildung 3: Visuelle Darstellung der geometrischen Ableitung der bewegungsspezifischen Koeffizienten. Nach der Spline-Interpolation der Körperachse werden die Segmente trigonometrisch berechnet, um ihre Veränderung über den zeitlichen Verlauf der Fortbewegung zu bestimmen. Die Abbildung wurde adaptiert von Taylor[2].
Das Modell wurde an der Bewegung von zwei schwimmenden Schlangen, der Ringelnatter Natrix natrix und der Gebänderten Wassernatter Nerodia fasciata pictiventris, einem mathematischen Modell von Nerodia nach Hertel[3] und an einem Butterfisch Centronotus gunnellus (Tab. 1). Für die Daten der peristaltischen Bewegung sei an dieser Stelle auf den Volltext dieser Arbeit verwiesen.
Tabelle 1: Liste der lokomotionsspezifischen Parameter und Koeffizienten für drei Organismen und ein mathematisches Modell nach Hertel[3].
| Nartrix natrix | Nerodia f. pictiventris | Math. Modell of Nerodia | Butterfisch Centronotus gunnellus | |
| Segmentanzahl | 30 | 30 | 30 | 20 |
| Segmentlänge [mm] | 8,5 | 8,5 | 3 | 6 |
| Segmentbreite [mm] | 1,732 | 1,732 | 1,732 | 1,732 |
| Halswirbelamplitude [%] | a=0,121s+1,658; s: 1-20 | a=0,056s+1,846; s: 1-15 | a=0,155s+4,723; s: 1-9 | a=0,242s+0,892; s: 1-20 |
| Brustwirbelamplitude [%] | - | - | a=0,001s+6,043; s: 9-15 | - |
| Lendenwirbelamplitude [%] | a=-0,301s+10.900 s: 20-30 | a=-0,062s+3,625; s: 15-30 | a=-0,085s+7,427; s: 15-30 | - |
| Schlagzyklus [s] | 0,31 | 0,21 | 0.21 | 0,45 |
| Verzögerung [s] s: 1-30 | v=-0,0005+0,0294 | v=-0,0004+0,0161 | v=-0,0004+0,0154 | v=-0,0014+0,0445 |
Um die Qualität des Modells bewerten zu können, werden die aus den Koeffizienten resultierenden Bewegungsmuster mit ihren natürlichen Vorbildern verglichen. Dabei zeigen die Simulationen, dass trotz der stark vereinfachten mathematischen Beschreibung, ein hoher Grad an Flexibilität und Abbildungstreue gewährleistet wird.
Ringelnatter Natrix natrix
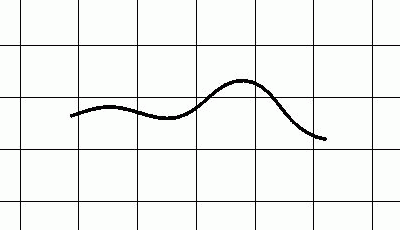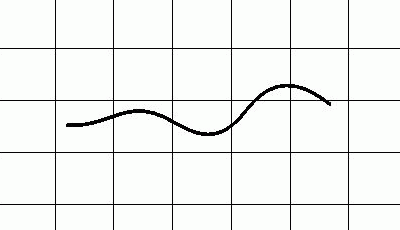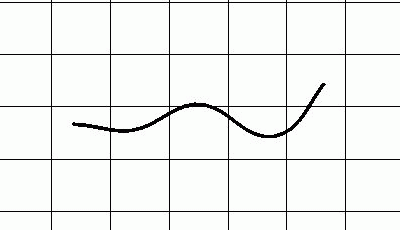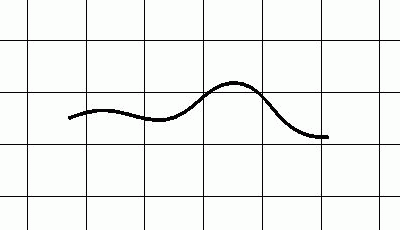
Simulation der schwimmenden Ringelnatter Natrix natrix auf Grundlage der mathematisch hergeleiteten Bewegungsparameter.
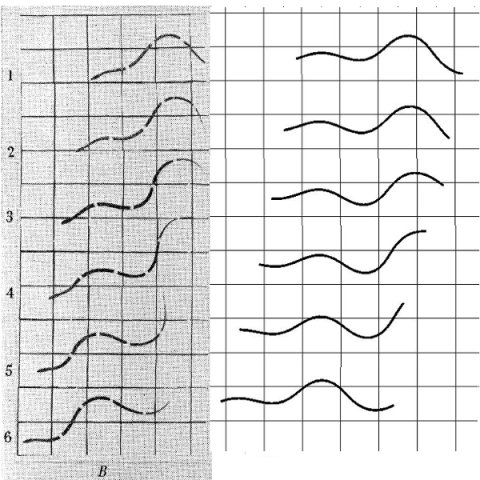
Vergleich des Bewegungsmusters der schwimmenden Ringelnatter Natrix natrix und dem Modell. Auf der linken Seite ist die Originalabbildung von Taylor[2] und auf der rechten Seite die Ergebnisse der Simulation dargestellt.
Wassernatter Nerodia fasciata pictiventris

Simulation einer schwimmenden Wassernatter Nerodia fasciata pictiventris auf Grundlage der mathematisch hergeleiteten Bewegungsparameter.
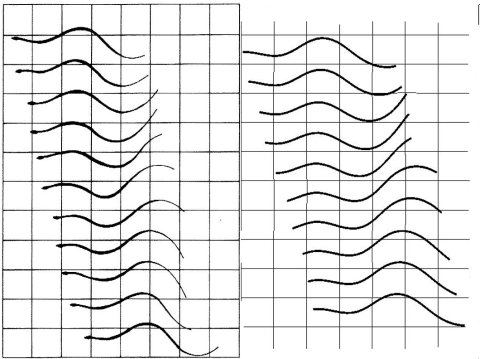
Vergleich der Fortbewegung der Wassernatter Nerodia f. pictiventris mit dem Modell. Auf der linken Seite ist die ursprüngliche Bildfolge von Jayne[4] und auf der rechten Seite die Bildfolge der Simulation dargestellt.
Mathematischen Modell von Nerodia
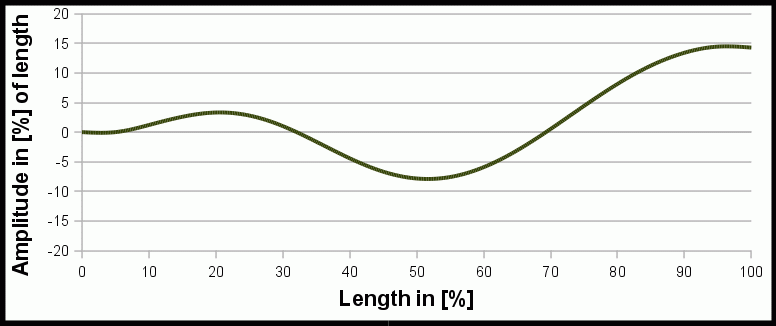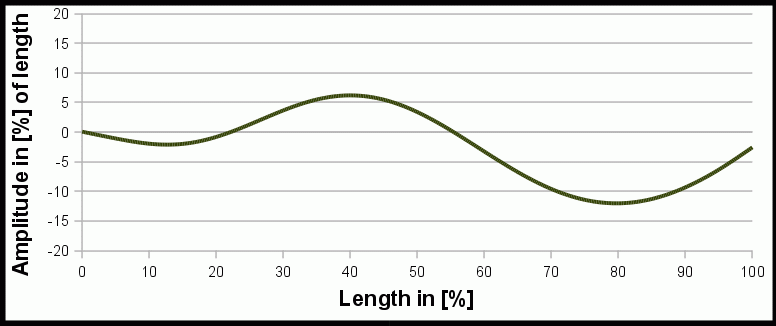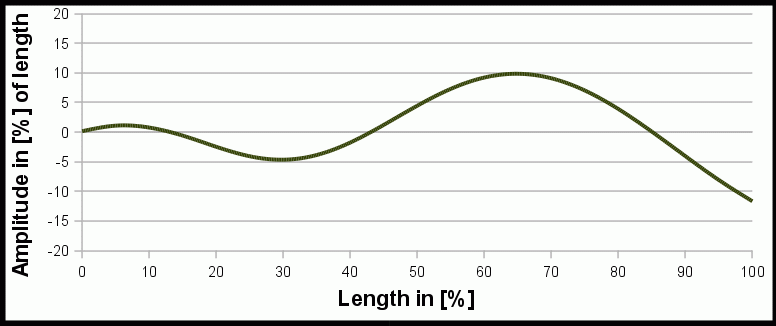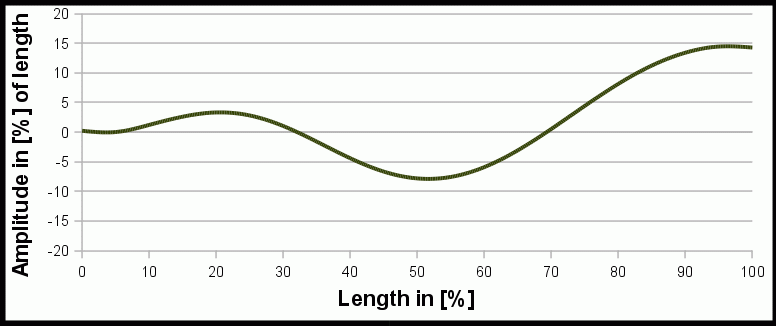
Animation des mathematischen Modells einer schwimmenden Wassernatter Nerodia f. pictiventris von Hertel[3].
Animation der schwimmenden Wassernatter Nerodia f. pictiventris basierend auf dem Segmentmodell.
Butterfisch Centronotus gunnellus
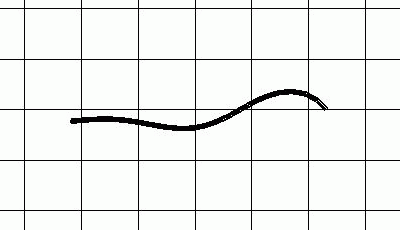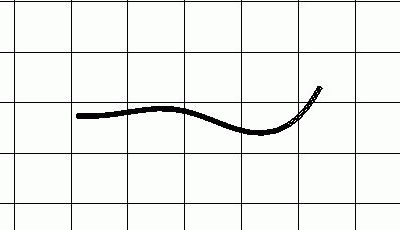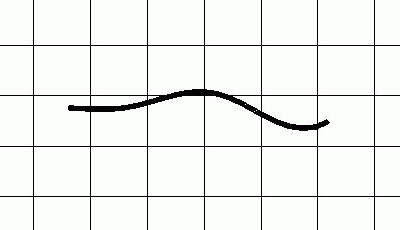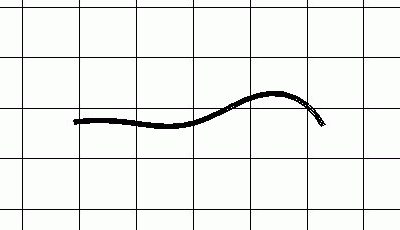
Simulation eines schwimmenden Butterfisch Centronotus gunnellus auf Grundlage der mathematisch hergeleiteten Bewegungsparameter.
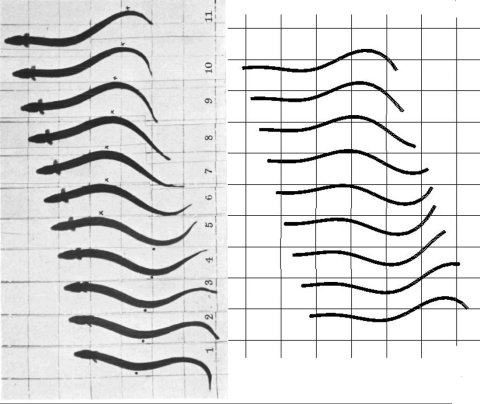
Vergleich eines schwimmenden Butterfisches Centronotus gunnellus. Das Originalbild von Gray[5] auf der linken Seite wird den Ergebnissen der Simulation auf der rechten Seite gegenübergestellt.
Die Ergebnisse zeigen ein äußerst flexibles System, das trotz ihrer einfachen Mathematik ein breites Anwendungsfeld für verschiedene gliedmaßenlose Fortbewegungsarten bietet. Anwendung könnte das System für die direkte Ansteuerung von Aktoren von Robotern, Antriebssystemen und in der Endoskopie finden, außerdem bietet es die Möglichkeit Wellenbewegungen verschiedener Organismen zu charakterisieren und zu klassifizieren.
References
[1] Alexander, R. M. (2003): Principles of Animal Locomotion, Princeton University Press, ISBN: 0-691-12634-8.
[2] Taylor, F. R. S. (1952): Analysis of the swimming of long and narrow animals, Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 214, No. 1117, pp. 158-183.
[3] Hertel, H. (1966): Structure-Form-Movement, Reinhold publishing corporation, New York.
[4] Jayne, B. C. (1985): Swimming in Constricting (Elaphe g. guttata) and Nonconstricting (Nerodia fasciata pictiventris) Colubrid Snakes, American Society of Ichthyologists and Herpetologists, pp.195-208.
[5] Gray, J. (1932): Studies in Animal Locomotion: I. The Movement of Fish with special Reference to the Eel, J. Exp. Biol. 10: 88-104.
last update: 08 Oct 2023 20:19
