 [Home] → [Projects] → [Schooling Fish]
[Home] → [Projects] → [Schooling Fish]
Please refer to the article on ResearchGate
Drag reduction in schooling fish – a CFD approach
Nils Owsianowski, Antonia B. Kesel
Bionik-Innovations-Centrum, Hochschule Bremen

There are different reasons why fish form schools. In addition to the aspects of protection, feeding and reproduction, schooling is also thought to improve the efficiency of locomotion. This hypothesis of energy saving through schooling has already been the subject of several studies[1,2]. As early as 1973, Weihs described typical patterns for schools of fish that cover large distances, especially during migration. According to his model, particularly advantageous constelations arise between individual fish. In order to avoid the high flow in the wake of a member of the group swimming ahead, one's own position is shifted sideways by about the width of the vortex street created. In this way, the drag can be reduced by up to 30 %, depending on the position of the fish in the school[3]. In this study, two-dimensional numerical simulations were carried out with up to nine individuals, focusing on flow conditions and interactions between individuals as well as the resistance distribution within the school. First, the behaviour of individual fish and the dynamics of a group were recorded experimentally. Using this information, an optimisation algorithm could be developed, which on the one hand simulates the mechanisms and the behaviour of a school, and on the other hand aims at a minimum total drag. Furthermore, dynamic simulations with moving grids show the numerical results of the undulating locomotion. Due to the undulating motion, an inverted van Kármán street is generated by the flow body. However, due to the greatly increased complexity of a dynamic calculation, an almost realistic model of a swimming school of fish was created.
Video 1: School of bass, recorded in the flow tank.
All iteration steps were calculated using CFD (Computational Fluid Dynamics), whose parameter control and evaluation was carried out by an evolutionary algorithm. Unstructured meshes with up to 60,000 elements were used (calculated in 2007). For the resolution of the boundary layer, at least ten prism layers were placed around the flow bodies. An "evolutionary strategy"[4] was chosen for the optimisation. It followed the steps of reproduction (copy of the previous generation), mutation (random variation) and selection (keeping the best formation) according to Charles Darwin's "survival of the fittest". In the present case, this means that the position of each individual was changed randomly (normally distributed random numbers), with the algorithm evaluating the resulting constellation in terms of the overall drag of the group. If the resistance to the previous arrangement is reduced, the new formation forms the basis for further evolutionary steps.
In order to test the system and evaluate its functionality, passive flow bodies were compared with results from flow tank experiments. The evolution of four bodies resulted in a straight alignment (Video 2) as the optimal pattern. Each flow body occupied a place directly behind the trailing edge of another flow body, with the exception of the leading one. We would actually expect such an arrangement, as there are many areas, especially in racing, where the use of slipstream is particularly advantageous.
Video 2: The result of a two-dimensional development of the arrangement of four passive streamlined bodies in relation to the minimum total drag. The colour scale shows the velocity progression from low (blue) to high velocity (red).
However, this does not apply to objects that are actively moving through a fluid. Due to the interaction between the swimming fish and its environment, the wake structure looks completely different. In order to move forward, the fish has to accelerate a certain amount of water backwards. As a result of this thrust generation, areas of the wake even exceed the cruising speed. Assuming the law of continuity, a uniformly swimming fish with constant velocity must compensate for its drag by generating exactly the same amount of thrust in the process. A simplified model of an actively swimming fish is a flow body that generates a thrust jet behind itself. Therefore, an additional velocity boundary condition was first implemented at the tail of the flow body. The resulting thrust was adapted to the respective flow resistance of the body so that the flow forces cancel each other out at constant speed. In simulations with four or six active flow bodies, clear diamond arrangements emerge, which show a slight offset to the respective leading positions (Video 3 & 4).
Video 3: Evolution of the swarm formation of four individuals.
Video 4: Evolution of the swarm formation of six individuals.
In a two-dimensional simulation, each flow body has two degrees of freedom (the x and y coordinates), so the number of possible constellations within an iteration step increases with the number of individuals. This is the weakness of an evolutionary strategy, because the number of generations required to reach an optimum also increases exponentially. There is also the possibility that the algorithm converges to a local optimum. Normally, an attempt to escape from such dead ends is achieved with a variable step size, but this additional parameter again increases the mutation possibilities. While an evolution of 4 fish still needs about 100 generations to reach the optimum, with 6 it is already about 400 generations. An evolution of 9 fish did not directly lead to an optimal constellation, so an additional approach of biological behaviour was implemented into the algorithm in this case. Three mechanisms are used; Firstly, only about a quarter of the entire group of fish performs a relevant position change at the same time. Secondly: If an individual swims in a particularly favourable position, it follows its leading conspecific. Thirdly: Interactions between individuals when there is a danger of collision. In this case, an individual moves aside to make way for an approaching fellow. Even with these three additional constraints, it took over 1500 generations to reach an optimum of 9 individuals. This also shows a clear diamond structure with slightly offset positions (Figure 1).
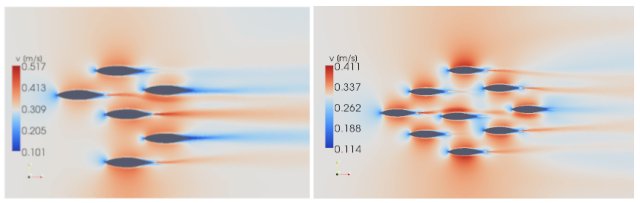
Figure 1: The results of the optimisations of six and nine individuals. The colour scale shows the velocity field in m/s. The velocity of the wake depends on the thrust generated. The higher the velocity, the higher the thrust generated and thus the resistance of a single group member.
A closer look at the drag distribution helps to better understand the mechanisms that form the structure of a school. A schematic representation of the resistance distribution can be seen in Figure 2. It shows that the resistance of an individual depends strongly on its position within the group. Surprisingly, the leading fish is not necessarily exposed to the highest drag, and furthermore, the drag can vary greatly between neighbouring individuals. This could be one reason for the dynamics and instability of schooling. Individuals frequently change their position, either to escape unpleasant spots or to stay in a favourable position.
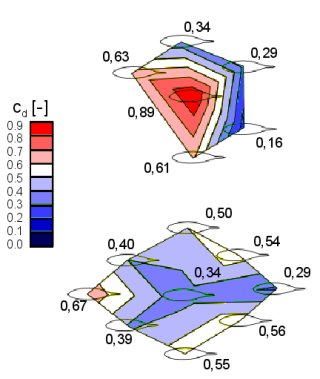
Abbildung 2: Schematic representation of the drag distribution within the school. The drag coefficient is indicated next to the respective position.
The jet propulsion model seems to be an acceptable simplification for simulating fish schools. However, the flow field of a swimming fish is much more complex. The next model considers the kinematics and wave-like motion of a swimming fish. For this purpose, the kinematics of a swimming fish were derived from video recordings and applied to a dynamically moving grid model. Video 5 shows the velocity field of a school of four individuals swimming in a diamond-shaped formation. It clearly shows the zigzag stream of the wake generated by the reverse van Kármán Street. It reveals not only the optimal position but also new questions about tail beat frequencies, amplitudes and wavelengths. In order to adjust the thrust generation required to compensate for the individual drag, the tail beat frequency was adjusted accordingly here.
Video 1: Dynamic CFD model of a swarm consisting of four individuals. Colour scale shows the velocity field.
References
[1] Belyayev, V. V. & Zuyev, G.V. (1969): Hydrodynamic hypothesis of school formation in fishes, Problems of Ichthyology: 9: 578-584.
[2] Partridge, B. L. (1983): The structure of schools of giant bluefin tuna in Cape Cod Bay, Exp. Biol. of Fishes: 9: 253-262.
[3] Weihs D. (1973): Hydrodynamics of Fish Schooling, Nature Vol. 241, 290-291.
[4] Rechenberg, I. (1994): Evolutionsstrategie ´94, Werkstatt Bionik und Evolutionstechnik, Band 1, Stuttgart: frommann-holzboog, ISBN: 3-7728-1641-X.
last update: 23 Nov 2023 19:00
