 [Home] → [Projects] → [Swimming snake]
[Home] → [Projects] → [Swimming snake]
Full text of the thesis is available on ResearchGate
Mathematical Modelling and Numerical Simulation of Locomotion of Limbless Organisms
In the course of evolution, different modes of locomotion have evolved ans each locomotion principle is perfectly adapted to its respective requirements, wings for flying, fins for swimming and legs provide a reasonable compromise for locomotion on land. Only snakes and worms have evolved limbless locomotion, which offers the possibility of getting around in different terrain with similar elegance[1]. They are almost independent of the environmental conditions, which makes the underlying principle of limbless locomotion interesting for technical applications. Before such a principle can be applied to technical systems, a general understanding of the underlying biomechanics and the associated mathematical description of the processes is necessary. This work takes the approach of a simple mathematical model derived from anatomy (musculoskeletal interaction) and the neuronal, cascading control of segmented organisms. It combines the advantages of wave movement of snakes and fishes with those of the peristaltic locomotion of worms. A key requirement is the simple description of the control pattern for the actuators in linear equations, so that small and inexpensive micro-controllers can process them quickly. The system of equations describes the respective movement patterns only by a series of coefficients that can be determined for the individual movement of an organism. Simulations illustrate the underlying model and provide the basis for a qualitative evaluation.
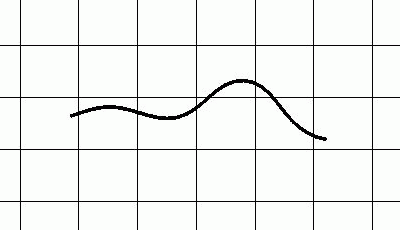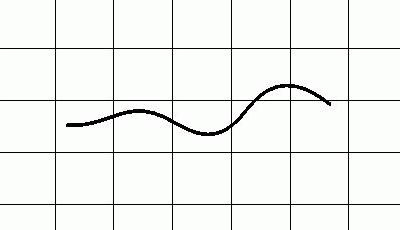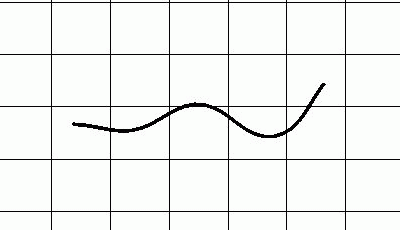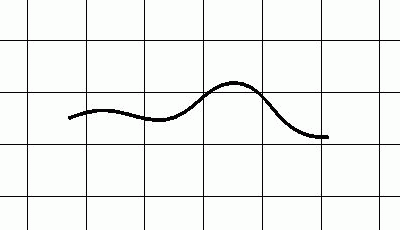
The concept is based on aligned triangular prisms (Fig. 1), whose longitudinal edges represent three actuators that tilt the end faces in cyclic stretches and contractions. To meet the requirements, the movement cycle is described as a simplified linear step function (Fig. 2).
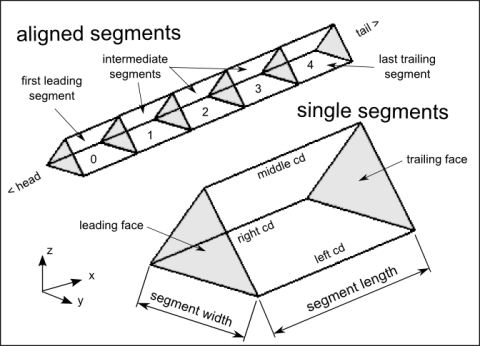
Figure 1: Illustration of the general construction plan of an artificial body segment. A segment is abstracted as a triangular prism with two triangular faces connected by three actuators cd. The assembly of several aligned segments results in the structure of a long and narrow model.
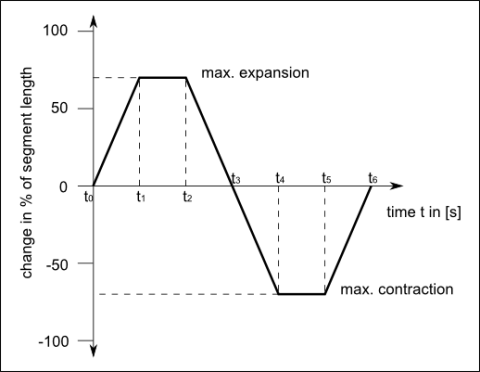
Figure 2: Principle of an expansion/contraction cycle of the actuators. The change in length is indicated relative to the original segment length and is plotted over time ti in seconds. The entire cycle is described by a section-wise defined function. Each section between two points ti and ti+1 is described by a linear function f(x)=mx+b.
These represent either vertebrates with a rigid skeletal element and two antagonistic muscle strands or three muscle strands that take over the function of the ring muscles of invertebrates. This allows both lateral entanglements and contractions of the segment to be depicted (Animation. 1). If the segments are attached to each other in a row and their successive, cyclic movements are delayed in time, undulation movements occur over the entire strand. Only two components are relevant for an individual, two-dimensional movement pattern. On the one hand, the degree of deformation, the amplitude, i.e. the strength of the stretching or contraction of the actuators. Secondly, the time delay of the movement cycle between two successive segments. Both components can change along the segment series.
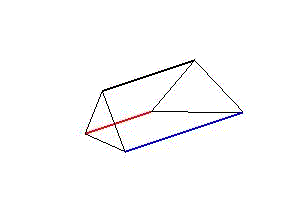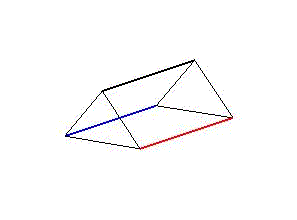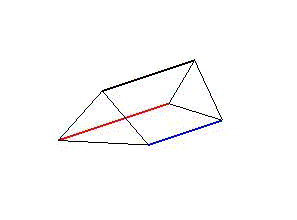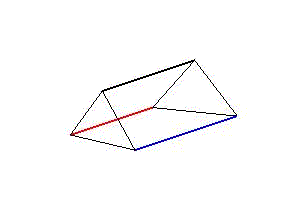
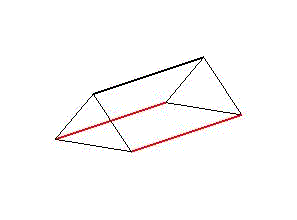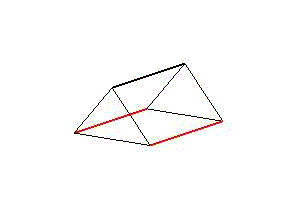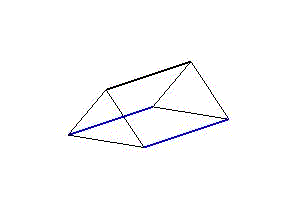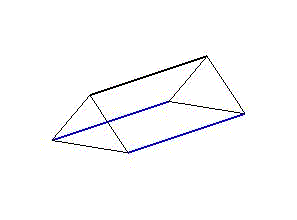
Animation 1: Schematic illustration of segment deformation during undulation on the left side and peristaltic movements on the right.
This change is assumed to be linear and is described in each case by two coefficients m and b in the equation f(x)=mx+b. While the change in the temporal delay is constant over the segment chain and is therefore described by a single function, the change in length is divided into three sections. There is the head section, the middle section and the tail section. Ultimately, these can be considered the three sections of the spine, which consists of the cervical, thoracic and lumbar sections. Thus, the amplitude of the deflection is determined via three equations with six coefficients, which are assigned to the respective segments. All coefficients can be derived geometrically from image sequences of recorded organisms. To do this, first the body axis is digitised, spline-interpolated and finally the segments are calculated trigonometrically. Their change over time can now be interpolated (Fig. 3). It is important to consider here that the length and width of the segments correspond to the dimensions of the later application.
![]()
Figure 3: Visual representation of the geometric derivation of the movement-specific coefficients. After spline interpolation of the body axis, the segments are calculated trigonometrically to determine their change over time during locomotion. The figure was adapted from Taylor[2].!
The model was tested on the movement of two swimming snakes, the grass snake Natrix natrix and the banded water snake Nerodia fasciata pictiventris, a mathematical model of Nerodia according to Hertel[3] and on a butterfish Centronotus gunnellus (Tab. 1). For the peristaltic movement data, please refer to the full text of this work.
Table 1: List of locomotion-specific parameters and coefficients for three organisms and a mathematical model according to Hertel[3].
| Nartrix natrix | Nerodia f. pictiventris | Math. model of Nerodia | Butterfish Centronotus gunnellus | |
| Number of segments | 30 | 30 | 30 | 20 |
| Segment length [mm] | 8,5 | 8,5 | 3 | 6 |
| Segment width [mm] | 1,732 | 1,732 | 1,732 | 1,732 |
| Cervical amplitude [%] | a=0,121s+1,658; s: 1-20 | a=0,056s+1,846; s: 1-15 | a=0,155s+4,723; s: 1-9 | a=0,242s+0,892; s: 1-20 |
| Thoracic vertebrae amplitude [%] | - | - | a=0,001s+6,043; s: 9-15 | - |
| Lumbar amplitude [%] | a=-0,301s+10.900 s: 20-30 | a=-0,062s+3,625; s: 15-30 | a=-0,085s+7,427; s: 15-30 | - |
| Beat cycle [s] | 0,31 | 0,21 | 0.21 | 0,45 |
| Delay [s] s: 1-30 | v=-0,0005+0,0294 | v=-0,0004+0,0161 | v=-0,0004+0,0154 | v=-0,0014+0,0445 |
In order to evaluate the quality of the model, the movement patterns resulting from the coefficients are compared with their natural models. The simulations show that despite the highly simplified mathematical description, a high degree of flexibility and fidelity is guaranteed.
Grass snake Natrix natrix
Simulation of the swimming grass snake Natrix natrix based on the mathematically derived movement parameters.
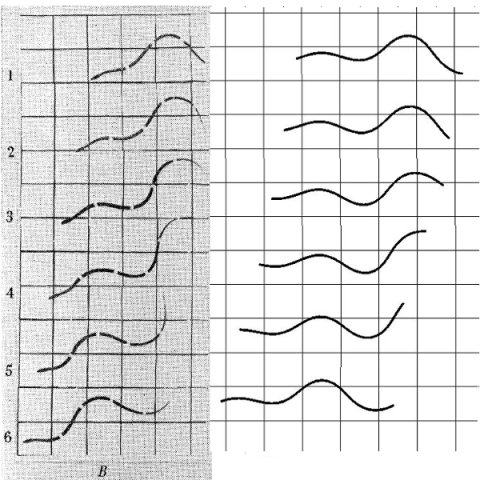
Comparison of the movement pattern of the swimming grass snake Natrix natrix and the model. The left side shows Taylor's[2] original illustration and the right side the results of the simulation.
Water snake Nerodia fasciata pictiventris
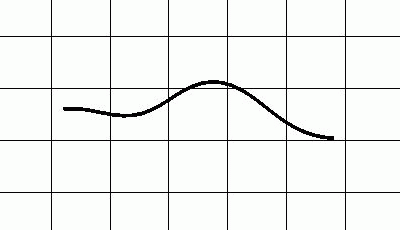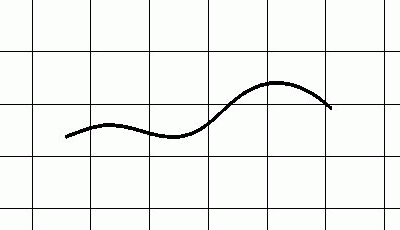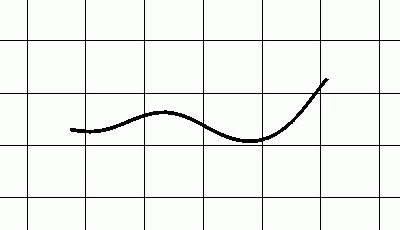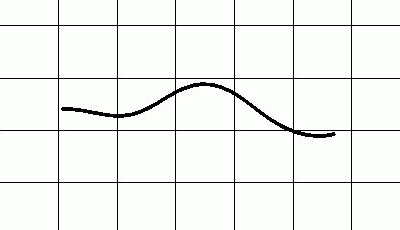
Simulation of a swimming water snake Nerodia fasciata pictiventris based on the mathematically derived movement parameters.
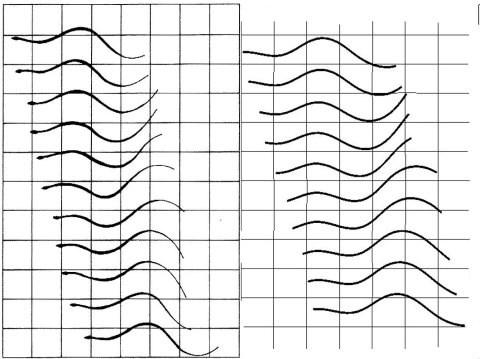
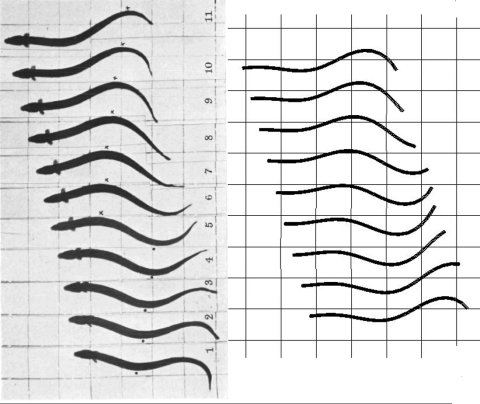
Comparison of the locomotion of the water snake Nerodia f. pictiventris with the model. The left side shows Jayne's[4] original image sequence and the right side the image sequence of the simulation.
Mathematical Model of Nerodia
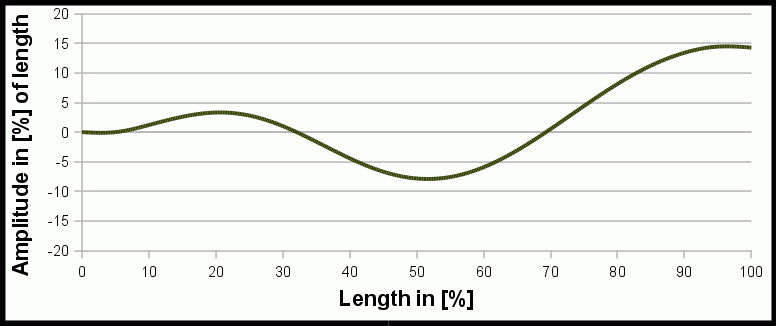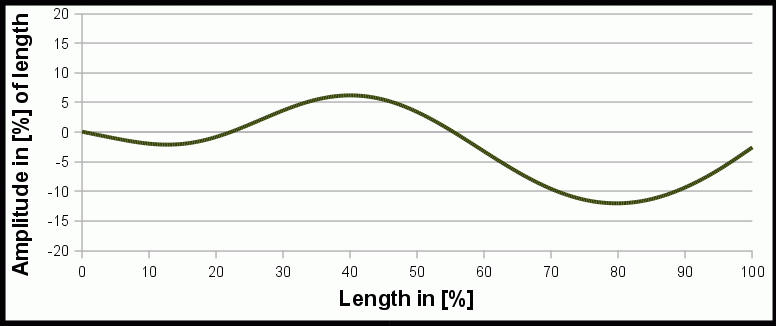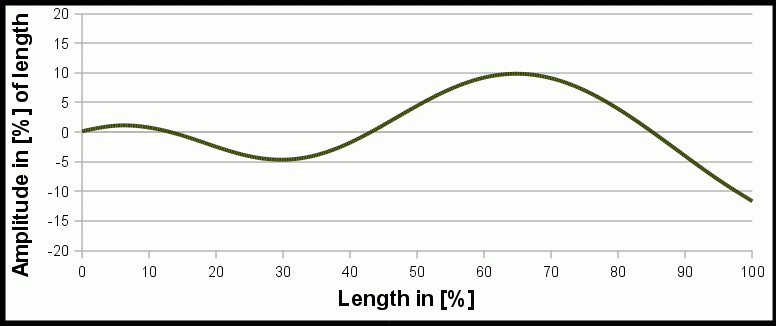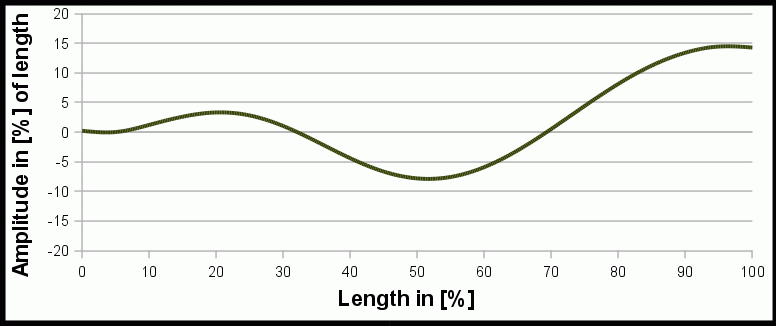
Animation of the mathematical model of a swimming water snake Nerodia f. pictiventris by Hertel[3].
Animation of the swimming water snake Nerodia f. pictiventris. based on the segment model.
Butterfish Centronotus gunnellus
Simulation of a swimming butterfish Centronotus gunnellus based on the mathematically derived movement parameters.
Comparison of a swimming butterfish Centronotus gunnellus. Gray's[5] original image on the left is compared with the results of the simulation on the right.
The results show an extremely flexible system that, despite its simple mathematics, offers a broad field of application for various limbless modes of locomotion. The system could be used for the direct control of actuators of robots, drive systems and in endoscopy, and it also offers the possibility to characterise and classify wave movements of different organisms.
References
[1] Alexander, R. M. (2003): Principles of Animal Locomotion, Princeton University Press, ISBN: 0-691-12634-8.
[2] Taylor, F. R. S. (1952): Analysis of the swimming of long and narrow animals, Royal Society of London. Series A, Mathematical and Physical Sciences, Vol. 214, No. 1117, pp. 158-183.
[3] Hertel, H. (1966): Structure-Form-Movement, Reinhold publishing corporation, New York.
[4] Jayne, B. C. (1985): Swimming in Constricting (Elaphe g. guttata) and Nonconstricting (Nerodia fasciata pictiventris) Colubrid Snakes, American Society of Ichthyologists and Herpetologists, pp.195-208.
[5] Gray, J. (1932): Studies in Animal Locomotion: I. The Movement of Fish with special Reference to the Eel, J. Exp. Biol. 10: 88-104.
last update: 08 Oct 2023 20:19
